高中數學反證法綜合測試題
一、選擇題
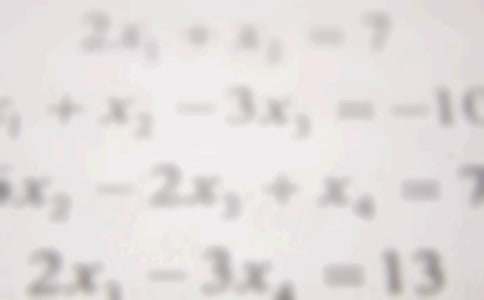
1.否定結論“至多有兩個解”的說法中,正確的是()
A.有一個解
B.有兩個解
C.至少有三個解
D.至少有兩個解
[答案] C
[解析] 在邏輯中“至多有n個”的否定是“至少有n+1個”,所以“至多有兩個解”的否定為“至少有三個解”,故應選C.
2.否定“自然數a、b、c中恰有一個偶數”時的正確反設為()
A.a、b、c都是奇數
B.a、b、c或都是奇數或至少有兩個偶數
C.a、b、c都是偶數
D.a、b、c中至少有兩個偶數
[答案] B
[解析] a,b,c三個數的奇、偶性有以下幾種情況:①全是奇數;②有兩個奇數,一個偶數;③有一個奇數,兩個偶數;④三個偶數.因為要否定②,所以假設應為“全是奇數或至少有兩個偶數”.故應選B.
3.用反證法證明命題“三角形的內角中至少有一個不大于60”時,反設正確的是()
A.假設三內角都不大于60
B.假設三內角都大于60
C.假設三內角至多有一個大于60
D.假設三內角至多有兩個大于60
[答案] B
[解析] “至少有一個不大于”的否定是“都大于60”.故應選B.
4.用反證法證明命題:“若整系數一元二次方程ax2+bx+c=0(a0)有有理根,那么a,b,c中至少有一個是偶數”時,下列假設正確的是()
A.假設a,b,c都是偶數
B.假設a、b,c都不是偶數
C.假設a,b,c至多有一個偶數
D.假設a,b,c至多有兩個偶數
[答案] B
[解析] “至少有一個”反設詞應為“沒有一個”,也就是說本題應假設為a,b,c都不是偶數.
5.命題“△ABC中,若B,則ab”的結論的否定應該是()
A.a
B.ab
C.a=b
D.ab
[答案] B
[解析] “ab”的否定應為“a=b或ab”,即ab.故應選B.
6.已知a,b是異面直線,直線c平行于直線a,那么c與b的位置關系為()
A.一定是異面直線
B.一定是相交直線
C.不可能是平行直線
D.不可能是相交直線
[答案] C
[解析] 假設c∥b,而由c∥a,可得a∥b,這與a,b異面矛盾,故c與b不可能是平行直線.故應選C.
7.設a,b,c(-,0),則三數a+1b,c+1a,b+1c中()
A.都不大于-2
B.都不小于-2
C.至少有一個不大于-2
D.至少有一個不小于-2
[答案] C
[解析] a+1b+c+1a+b+1c
=a+1a+b+1b+c+1c
∵a,b,c(-,0),
a+1a=--a+-1a-2
b+1b=--b+-1b-2
c+1c=--c+-1c-2
a+1b+c+1a+b+1c-6
三數a+1b、c+1a、b+1c中至少有一個不大于-2,故應選C.
8.若P是兩條異面直線l、m外的任意一點,則()
A.過點P有且僅有一條直線與l、m都平行
B.過點P有且僅有一條直線與l、m都垂直
C.過點P有且僅有一條直線與l、m都相交
D.過點P有且僅有一條直線與l、m都異面
[答案] B
[解析] 對于A,若存在直線n,使n∥l且n∥m
則有l∥m,與l、m異面矛盾;對于C,過點P與l、m都相交的直線不一定存在,反例如圖(l∥);對于D,過點P與l、m都異面的直線不唯一.
9.有甲、乙、丙、丁四位歌手參加比賽,其中只有一位獲獎,有人走訪了四位歌手,甲說:“是乙或丙獲獎”,乙說:“甲、丙都未獲獎”,丙說:“我獲獎了”,丁說:“是乙獲獎了”,四位歌手的話只有兩句是對的,則獲獎的歌手是()
A.甲
B.乙
C.丙
D.丁
[答案] C
[解析] 因為只有一人獲獎,所以丙、丁只有一個說對了,同時甲、乙中只有一人說對了,假設乙說的對,這樣丙就錯了,丁就對了,也就是甲也對了,與甲錯矛盾,所以乙說錯了,從而知甲、丙對,所以丙為獲獎歌手.故應選C.
10.已知x10,x11且xn+1=xn(x2n+3)3x2n+1(n=1,2…),試證“數列{xn}或者對任意正整數n都滿足xnxn+1,或者對任意正整數n都滿足xnxn+1”,當此題用反證法否定結論時,應為()
A.對任意的正整數n,都有xn=xn+1
B.存在正整數n,使xn=xn+1
C.存在正整數n,使xnxn+1且xnxn-1
D.存在正整數n,使(xn-xn-1)(xn-xn+1)0
[答案] D
[解析] 命題的結論是“對任意正整數n,數列{xn}是遞增數列或是遞減數列”,其反設是“存在正整數n,使數列既不是遞增數列,也不是遞減數列”.故應選D.
二、填空題
11.命題“任意多面體的面至少有一個是三角形或四邊形或五邊形”的結論的否定是________.
[答案] 沒有一個是三角形或四邊形或五邊形
[解析] “至少有一個”的否定是“沒有一個”.
12.用反證法證明命題“a,bN,ab可被5整除,那么a,b中至少有一個能被5整除”,那么反設的內容是________________.
[答案] a,b都不能被5整除
[解析] “至少有一個”的否定是“都不能”.
13.用反證法證明命題:“一個三角形中不能有兩個直角”的過程歸納為以下三個步驟:
①A+B+C=90+90+180,這與三角形內角和為180相矛盾,則A=B=90不成立;
②所以一個三角形中不能有兩個直角;
③假設A,B,C中有兩個角是直角,不妨設A=B=90.
正確順序的序號排列為____________.
[答案] ③①②
[解析] 由反證法證明的`步驟知,先反證即③,再推出矛盾即①,最后作出判斷,肯定結論即②,即順序應為③①②.
14.用反證法證明質數有無限多個的過程如下:
假設______________.設全體質數為p1、p2、…、pn,令p=p1p2…pn+1.
顯然,p不含因數p1、p2、…、pn.故p要么是質數,要么含有______________的質因數.這表明,除質數p1、p2、…、pn之外,還有質數,因此原假設不成立.于是,質數有無限多個.
[答案] 質數只有有限多個 除p1、p2、…、pn之外
[解析] 由反證法的步驟可得.
三、解答題
15.已知:a+b+c0,ab+bc+ca0,abc0.
求證:a0,b0,c0.
[證明] 用反證法:
假設a,b,c不都是正數,由abc0可知,這三個數中必有兩個為負數,一個為正數,
不妨設a0,b0,c0,則由a+b+c0,
可得c-(a+b),
又a+b0,c(a+b)-(a+b)(a+b)
ab+c(a+b)-(a+b)(a+b)+ab
即ab+bc+ca-a2-ab-b2
∵a20,ab0,b20,-a2-ab-b2=-(a2+ab+b2)0,即ab+bc+ca0,
這與已知ab+bc+ca0矛盾,所以假設不成立.
因此a0,b0,c0成立.
16.已知a,b,c(0,1).求證:(1-a)b,(1-b)c,(1-c)a不能同時大于14.
[證明] 證法1:假設(1-a)b、(1-b)c、(1-c)a都大于14.∵a、b、c都是小于1的正數,1-a、1-b、1-c都是正數.(1-a)+b2(1-a)b>14=12,
同理(1-b)+c2>12,(1-c)+a2>12.
三式相加,得
(1-a)+b2+(1-b)+c2+(1-c)+a2>32,
即32>32,矛盾.
所以(1-a)b、(1-b)c、(1-c)a不能都大于14.
證法2:假設三個式子同時大于14,即(1-a)b14,(1-b)c14,(1-c)a14,三式相乘得
(1-a)b(1-b)c(1-c)a143①
因為01,所以0a(1-a)1-a+a22=14.
同理,0b(1-b)14,0c(1-c)14.
所以(1-a)a(1-b)b(1-c)c143.②
因為①與②矛盾,所以假設不成立,故原命題成立.
17.已知函數f(x)是(-,+)上的增函數,a,bR.
(1)若a+b0,求證:f(a)+f(b)f(-a)+f(-b);
(2)判斷(1)中命題的逆命題是否成立,并證明你的結論.
[解析] (1)證明:∵a+b0,a-b.
由已知f(x)的單調性得f(a)f(-b).
又a+bb-af(b)f(-a).
兩式相加即得:f(a)+f(b)f(-a)+f(-b).
(2)逆命題:
f(a)+f(b)f(-a)+f(-b)a+b0.
下面用反證法證之.
假設a+b0,那么:
a+ba-bf(a)f(-b)a+bb-af(b)f(-a)
f(a)+f(b)f(-a)+f(-b).
這與已知矛盾,故只有a+b0.逆命題得證.
18.(2010湖北理,20改編)已知數列{bn}的通項公式為bn=1423n-1.求證:數列{bn}中的任意三項不可能成等差數列.
[解析] 假設數列{bn}存在三項br、bs、bt(rt)按某種順序成等差數列,由于數列{bn}是首項為14,公比為23的等比數列,于是有btbr,則只可能有2bs=br+bt成立.
21423s-1=1423r-1+1423t-1.
兩邊同乘3t-121-r,化簡得3t-r+2t-r=22s-r3t-s,
由于rt,所以上式左邊為奇數,右邊為偶數,故上式不可能成立,導致矛盾.
故數列{bn}中任意三項不可能成等差數列.
【高中數學反證法綜合測試題】相關文章:
1.高中數學組合綜合測試題以及答案
2.高中數學數列綜合試題
3.小學數學期中綜合測試題
4.職稱日語考試A級綜合測試題
5.高考歷史綜合檢測試題與答案
6.2017執業藥師藥學綜合知識預測試題
7.執業藥師《藥學綜合知識》自測試題
8.2017年高考《語文》綜合測試題