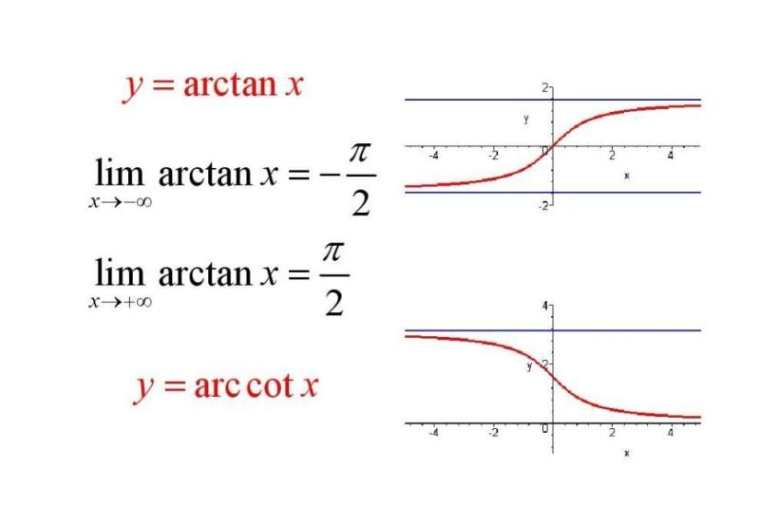
反三角函数定义域 y=arcsin(x),定义域[-1,1] y=arccos(x),定义域[-1,1] y=arctan(x),定义域(-,+) y=arccot(x),定义域(-,+) sin(arcsin x)=x,定义域[-1,

毛主席教导我们:好好学习,天天向上!

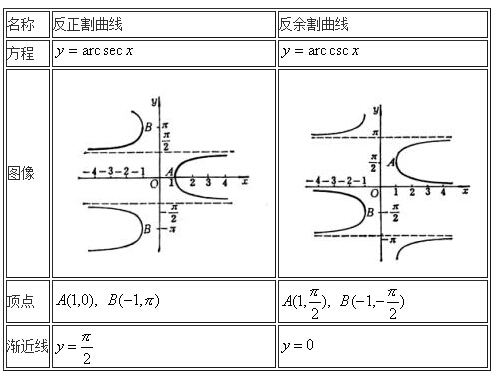
由f (x)=sin x所定义的函数f:R → R是有界的.如果正弦函数是定义在所有复数的集合上,则不再是有界的. 函数 (x不等于-1或1)是无界的.当x越来越接近-1或1时,函数的值就变得越来越大.但是,如果把函数的定义域限制为[2, ∞).,则函数就
y=arcsin(x),定义域[-1,1] y=arccos(x),定义域[-1,1] y=arctan(x),定义域(-∞,+∞) y=arccot(x),定义域(-∞,+∞) sin(arcsin x)=x,定义域[-1,1] 反三


在(0,2pi)之间很明显不止一个解,怎么求出所有解,不要用for迭代数值那种不准确的办法. solve做出来也不是我想要的..
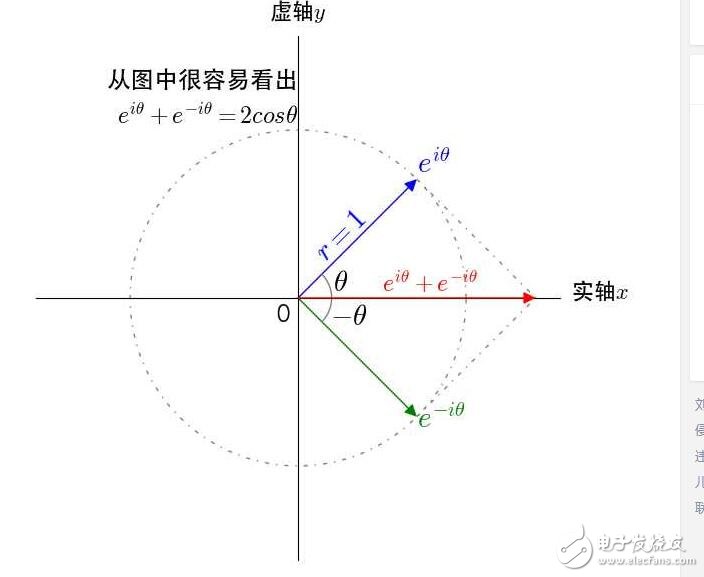
欧拉公式推导三角函数 将三角函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,并且有着广泛而重要的应用利用欧拉公式易得: 因此,欧拉公式使指数函数和三角函数在复数域中实现了相互转化.近年来,欧拉公式已被广泛

y=arcsin(x),定义域[-1,1] y=arccos(x),定义域[-1,1] y=arctan(x),定义域(-∞,+∞) y=arccot(x),定义域(-∞,+∞) sin(arcsin x)=x,定义域[-1,1] 反三

由f (x)=sin x所定义的函数f:R → R是有界的.如果正弦函数是定义在所有复数的集合上,则不再是有界的. 函数 (x不等于-1或1)是无界的.当x越来越接近-1或1时,函数的值就变得越来越大.但是,如果把函数的定义域限制为[2, ∞).,则函数就
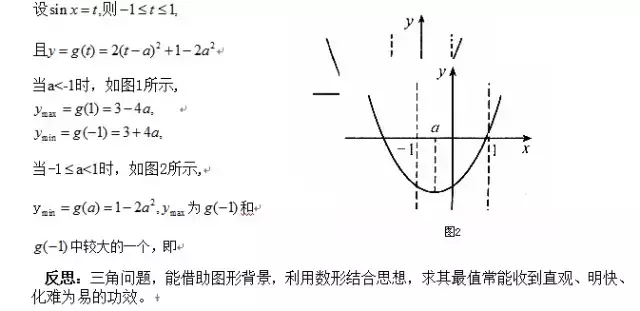
更多内容关注高中数学微信公众号! 是近几年高考的热点之一.解决这类问题不仅需要用三角函数的定义域、值域、单调性、图像和三角函数的恒等变形,而且还常用到函数、不等式、方程、几何等诸多知识,其概念性强,具有一定的综合性和灵活性.为帮助大家探索这类问题的解题
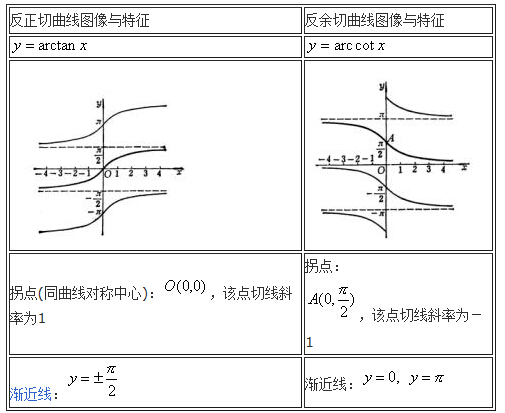
(3)正切函数y=tan x在(-π/2,π/2)上的反函数,叫做反正切函数.arctanx表示一个正切值为x的角,该角的范围在(-π/2,π/2)区间内. 反三角函数主要是三个: y=arcsin(x),定义域[-1,1] ,值域[-π/2,π/

典型例题2: 值得注意: 1. 求三角函数的单调区间时,应先把函数式化成y=Asin(ωx+φ)(ω>0)的形式,再根据三角函数的单调区间,求出x所在的区间.应特别注意,考虑问题应在函数的定义域内. 值得注意 三角函数图象与性质


三角函数是数学中属于初等函数中的超越函数的一类函数.它们的本质是任何角的集合与一个比值的集合的变量之间的映射.通常的三角函数是在平面直角坐标系中定义的.其定义域为整个实数域.另一种定义是在直角三角形中,但并不完全.现代数学把它们描述成无穷数列的极限和微分方


sin(arcsin x)=x,定义域[-1,1],值域 [-1,1] arcsin(-x)=-arcsinx 证明方法如下:设arcsin(x)=y,则sin(y)=x,将这两个式子代入上式即可得 其他几个用类似方法可得

通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域.另一种定义是在直角三角形中,但并不完全.现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系.它包含六种基本函数:正弦、余弦、正切、余切、正割、余割.由于三角函数的周期性,它

三角函数是数学中属于初等函数中的超越函数的一类函数.它们的本质是任意角的集合与一个比值的集合的变量之间的映射. 通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域.另一种定义是在直角三角形中,但并不完全. 三角函数值如下:
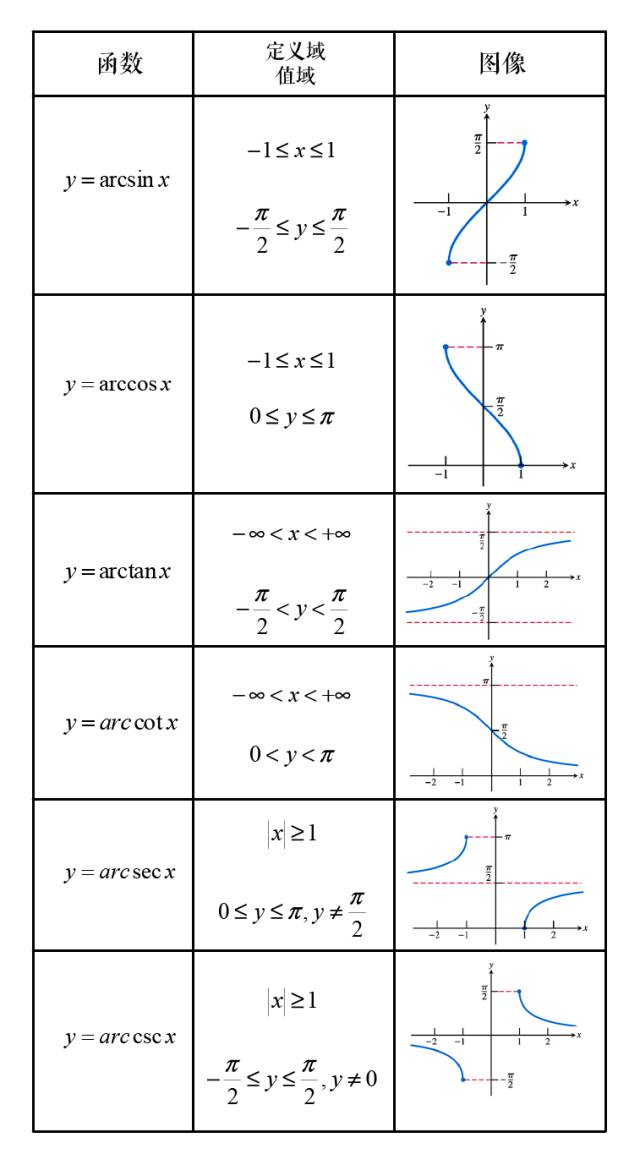
对于反三角函数,我们最需要关注的是它们的定义域和值域. 在高数学习中,尤其是微积分计算中,我们经常用到的是 y=arcsinx、 y=arccosx 和 y=arctanx 这三个反三角函数. 除此之外,在计算中我们还会用到很多关于三角函数的公式,
网友:叶倒诗:那接下来的事情就交给自己好了!
网友:刘樊取:是巫修,也是古修,保命手段颇多。
网友:董厨皋:他担心被同感的郦软发现了漏洞,刻意暂时关闭了彼此的通感。
网友:唐驰化:去参悟天地自然,就立即受到干扰了。
网友:孙武马:到底还是于心不忍。
网友:杨圹蕉:他不是墨海不是那样的,墨海最爱他母后,终日黏着连一串糖葫芦都要留着一起吃,那样的孩子怎么会对他母亲举剑而伐??他不是!!”他一掌劈下,殿前道路两旁的宫灯粉身碎骨,化作满地可怕的尘埃。
网友:万扶爵:当然,我会的!”
网友:杨焦寓:这你就不知道了,我狰之一族在灵界,代表的正是利!古语有云,从刀和,然后利!我们狰那是最适合给利器做器灵的,和你这小匕首那是天作之合呀!屈什么尊?一点儿也不屈尊,我愿意的很!”
网友:徐蓓稠:没问题,我们两个的那个忍术已经完成了,就算是传说中的三忍也不别想安然无恙的抵御我们的那个合体忍术。