

第1题第①问分析:给出了tanα的值,来求一个含有正弦余弦的代数式,明显需要把正余弦化为正切,下面要讲的是弦化切最常见的方法,分母是弦的2次式,只需要把分子1写成sin2α+cos2α,这样分子分母都是关于弦的2次式子,然后分子分母同时除以cos2α,就可


齐次化切在三角计算中经常会遇到,遇切化弦也是,都是为了便于解题

欢迎关注微信公众号\"许兴华数学\": (4)使式中的分母尽量不含有三角函数; (5)使式中尽量不含有根号和绝对值符号; (6)能求值的,要求出具体的值,否则就用三角函数式来表示.

方法一:弦化切.已知给出了tanα的值,要求的表达式中的每一项都是正弦余弦的二次项,所以可以考虑使用弦化切的方法来求解,如下,先把式子写成分母为1的分式形式,然后分子和分母同时除以cos 2α,则整个式子中的三角函数全部变成了tanα,之后代值就可以了;这

切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等
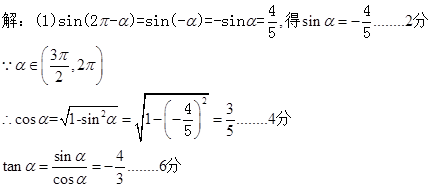
考点:本试题考查了三角函数的化简和求值. 点评:对于三角函数中的求值问题,解决试题的关键是对于其的化简,而化简的一般思路是切化弦,然后同一三角名称,借助于三角函数的同角关系式来求解和运算,他那哦故事要助于平方关系中开根号要注意符号问题,这是个易错点,容
更多解题技巧请观看视频: 三角函数化简绝招---全面突破化简软肋 3、降幂:但不能违背统一角的原则 4、遇到特殊角拆 5、边转角,角转变 6、归一原则 7、配角原则 今天重点分享切化弦以及边转角和角转变

只要切化弦,然后往下算就行了.注意sin80 化成cos10,sin50 化为cos40

三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构.即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常\"切化弦\";第三观察代数式的结构特点.基本的技巧有: 两角和与差的正弦、余弦

第③问分析:先把代数式书写成分母为1的分式形式,同时把1改写为sin2α+cos2α,然后分子分母同时除以cos2α,如下图,之后分子中还含有弦:sinαcosα,只需要使用同样的方法把sinαcosα化为正切即可,详细过程如下: 就可以使用这种方法把

)(填 号) 一般情况下: 、二倍角公式中的倍数关系是相对的,为深化对二倍角公式的理解,出示一组填空题(放幻灯片) )填角

切化弦是什么?这一步怎么来的?

第2题分析:题中同时存在弦和切时,如果找不到更好的方法,一般考虑先把切化为弦,再做打算,如①;有分式相加,通分使之变成单个的分式,如②;看到分式的分子这种形式,就该想到可以使用和差公式把分子变形成单个的三角函数,如③;到这儿,本题基本上就可以顺利做出来了,

这种题目一般思路都是切化弦,注意到两个角之间的关系
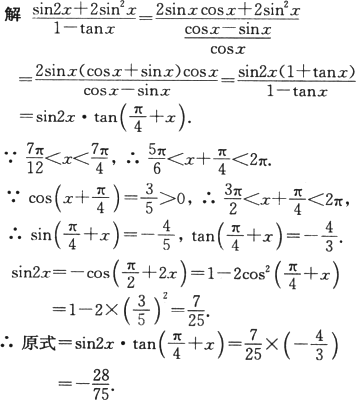
点评:待求式由切化弦入手,得出tan 的角与条件式相吻合,而sin2x的值则由诱导公式和倍角公式来完成,这种条件求值的解题思路应学会掌握. 练习册系列答案 答案: 解析:

切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等变换课件 切化弦 三角恒等

二、三角恒等变换的常见形式 三角恒等变换中常见的三种形式:一是化简;二是求值;三是三角恒等式的证明. 1、三角函数的化简常见的方法有切化弦、利用诱导公式、同角三角函数关系式及和、差、倍角公式进行转化求解. 2、三角函数求值分为给值求值(条件求值)与给角求值

三、三角函数式的化简要遵循\"三看\"原则 1、一看\"角\",这是最重要的一环,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式; 2、二看\"函数名称\",看函数名称之间的差异,从而确定使用的公式,常见的有\"切化弦\"; 3、三看\"结构特征\",分析结构
网友:毛岑舟:因为她变幻的童子模样并不未见过,出言尚算客气。
网友:李仅戏:在张青山的心中,最值得信任的,就是郑忠祥。
网友:姜怀:那就是帮助之人可能会遭打天道反噬,轻则仙法受损,重则劫难会十倍、百倍的转架到他的身上。
网友:段娜尼: 苏河点了点头,淡淡道:“那你就去死吧。
网友:范戏书:传遍周围诸多宇宙。